Physics assignment
Classical mechanics
Problem statement
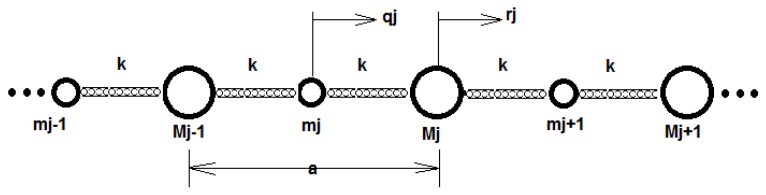
Particles with two different masses m and M are located along a linear harmonic chain
of infinite length. The chain has a force constant k (see the picture below). The
distance between two particles with the same mass is equilibrium and equals to a.
qj and rj are the deviations of particles mj and Mj from their equilibrium positions respectively.
-
- Find both potential and kinetic energies of the system and the Lagrangian of the
system. Write down the equations of motion for qi and ri. - If the equations
![Rendered by QuickLaTeX.com q_{j}=Q_{j}\exp{[i{\omega}t]}](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-ba94f9892ed02c6e67626f7388b24ea9_l3.png) and
and ![Rendered by QuickLaTeX.com r_{j}=R_{j}\exp{[i{\omega}t]}](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-6a255c3c06129d949dcce3e65b68cf54_l3.png) are applied, what are the equations for the amplitudes Qj and Rj?
are applied, what are the equations for the amplitudes Qj and Rj? - Let
![Rendered by QuickLaTeX.com Q(k)=\sum_{j=-\infty}^{j=+\infty}{Q_{i}\exp[i(jka)]}](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-d897037da43368ea269bfba6e04a7d22_l3.png) and
and ![Rendered by QuickLaTeX.com R(k)=\sum_{j=-\infty}^{j=+\infty}{R_{j}\exp[i(jka)]}](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-2dabe17b03890e257da51ec403080436_l3.png) , where
, where 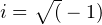 and the sum on j is over all particles of mass m for Q(k) or over all particles of mass M for R(k). Perform the sum over all of the amplitudes in part 2) above and determine the equations for Q(k) and R(k) using the above definitions for Q(k) and R(k).
and the sum on j is over all particles of mass m for Q(k) or over all particles of mass M for R(k). Perform the sum over all of the amplitudes in part 2) above and determine the equations for Q(k) and R(k) using the above definitions for Q(k) and R(k). - Determine the normal mode frequencies
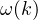 for the system, where
for the system, where ![Rendered by QuickLaTeX.com k\in[-\pi/(2a),+\pi/(2a)]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-1f8e111ed7937ac3ed7b6740c0b19969_l3.png) .
.
- Find both potential and kinetic energies of the system and the Lagrangian of the
Solution
- The kinetic energy of the system can be determine from the equation below:
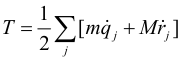
The potential energy of the system can be found from the equation below:
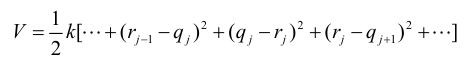
The Lagrangian can be found as follows:
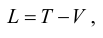 Where T is the kinetic energy and V is the potential energy, determined above.
Where T is the kinetic energy and V is the potential energy, determined above.
The equations of motion for jth points can be found as the partial differentials from the
Lagrangian:
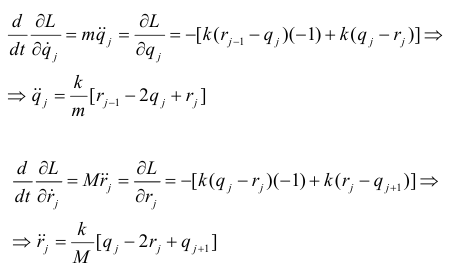
- Let
![Rendered by QuickLaTeX.com q_{j}=Q_{j}\exp{[i({\omega}t})]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-dc3a330e2d02feeb05af554357685e81_l3.png) with
with ![Rendered by QuickLaTeX.com Q(k)=\sum_{j=-\infty}^{j=+\infty}{Q_{i}\exp[ijka]}](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-a7370998f86b2f1ade8482845e10a16e_l3.png) and
and ![Rendered by QuickLaTeX.com r_{j}=R_{j}\exp{[i({\omega}t)]}](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-a9193406967aecaa1ae03933ac1337ab_l3.png) with
with ![Rendered by QuickLaTeX.com R(k)=\sum_{j=-\infty}^{j=+\infty}{R_{j}\exp[ijka]}](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-ac06256ce0337a2dc035b1602a9138d6_l3.png) .Then
.Then ![Rendered by QuickLaTeX.com \"{q}_{j}=-\omega^2Q_{j}\exp[i(\omega{t})]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-9f49038691aaf1c3459f29f0e2b1af18_l3.png) and
and ![Rendered by QuickLaTeX.com \"{r}_{j}=-\omega^2R_{j}\exp[i(\omega{t})]](https://assignmentshark.com/blog/wp-content/ql-cache/quicklatex.com-be801cd5bf1085d22e995e96d75fe304_l3.png) .
.
Therefore,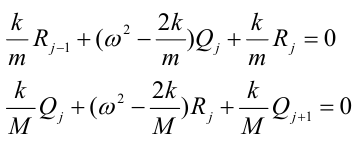
- In order to find the solution for part 3, multiplication by exp[i(jka)] should be
performed.
Therefore,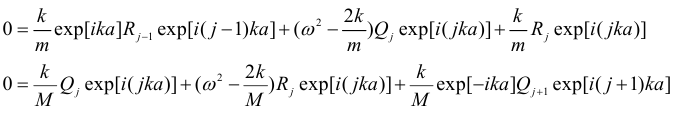 Applying the differentiation for Q(k), R(k) enables to sum over j:
Applying the differentiation for Q(k), R(k) enables to sum over j: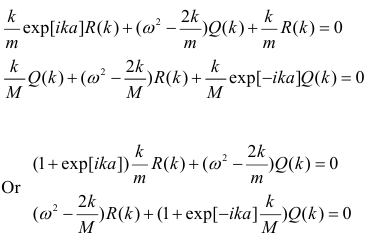
- For non-trivial solutions Q(k) and R(k), the determinant, as shown below, should
be equal to zero.
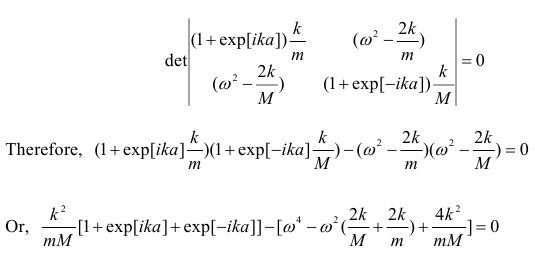
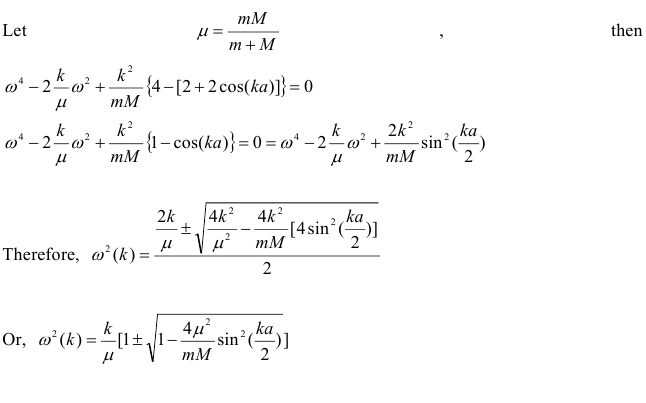
Physics Assistance from the Experts
You have come to the right place if you look for physics problem solver online. You can search our blog to find more examples and articles related to physics study hacks, or place your order and get rid of all of your worries once and for all. We work with all kinds of assignments and all disciplines, from high school to advanced university studies. We know that sometimes being a student and trying to keep a descent GPA can be really hard. We are here with a team of professionals to help with assignments you and provide you with solved problems in physics, mathematics, chemistry or any other discipline you need.
Here is one more physics sample paper that can be helpful in your studies.