Dijkstra’s shortest path algorithm finds the shortest paths between all nodes of the graph. In this article we will describe the operation principle of Dijkstra’s algorithm, which finds optimal routes. The disadvantage of this algorithm is that it will not work correctly if the graph has negative edge weights. In this tutorial you can read Dijkstra’s shortest path algorithm example. The author has solved a particular task and provided a vivid description of the solution. Following each step you will be able to solve a similar solution by yourself with ease.
With our Dijkstra’s shortest path algorithm example you can learn how to create and solve similar tasks. Look attentively to each step and highlight the important points that you need to consider while solving such an assignment. On our blog you can find various samples connected with this and other topics. Our service helps hundreds of students that have troubles with assignments in various disciplines: programming, mathematics, chemistry, physics, statistics, and more. If for some reason you can’t manage the assignment by yourself you can ask our writers for online assignment help.
Dijkstra’s Shortest Path Algorithm Task
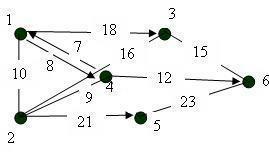
Task: find all the shortest paths from the vertex # 1 for the graph shown in the figure below using the Dijkstra algorithm.
Solution:
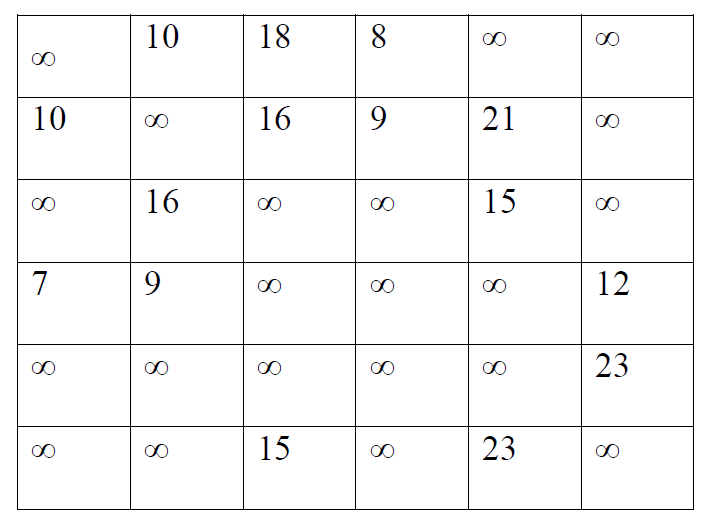
First, we form the matrix of lengths of shortest arcs for a given graph.
The starting vertex from which the tree of shortest paths is constructed is the vertex 1.
We set the starting conditions:
![]()
We color vertex 1, ![]() .
.
We find the nearest vertex to the one that was colored by us, using the formula:
![]()
![]()
![]()
![]()
![]()
The minimum length has a path from vertex 1 to vertex 4 ![]() . We include the vertex # 4 in the current oriented tree, as well as the arc leading to this vertex.
. We include the vertex # 4 in the current oriented tree, as well as the arc leading to this vertex.
![]()
![]()
![]()
![]()
The minimum length is the path from vertex 1 to vertex 2 ![]() . We include vertex # 2 in the current oriented tree, as well as the arc leading to this vertex. According to the expression this is the arc (1,2).
. We include vertex # 2 in the current oriented tree, as well as the arc leading to this vertex. According to the expression this is the arc (1,2).
![]()
![]()
![]()
The minimum length is the path from vertex 1 to vertex 3 ![]() . We include vertex # 3 in the current oriented tree, as well as the arc leading to this vertex. According to the expression, this is the arc (1.3).
. We include vertex # 3 in the current oriented tree, as well as the arc leading to this vertex. According to the expression, this is the arc (1.3).
![]()
![]()
The minimum length is the path from vertex 1 to vertex 6 ![]() . We include the vertex # 6 in the current oriented tree, as well as the arc leading to this vertex. According to the expression, this is the arc (4.6).
. We include the vertex # 6 in the current oriented tree, as well as the arc leading to this vertex. According to the expression, this is the arc (4.6).
![]()
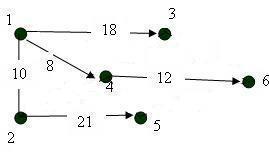
The minimum length is the path from vertex 1 to vertex 5 ![]() . We include vertex # 5 in the current oriented tree, as well as the arc leading to this vertex. According to the expression, this is the arc (2.5). We have obtained an oriented tree of the shortest paths starting at vertex # 1 for the original graph.
. We include vertex # 5 in the current oriented tree, as well as the arc leading to this vertex. According to the expression, this is the arc (2.5). We have obtained an oriented tree of the shortest paths starting at vertex # 1 for the original graph.
![]() The length of the route
The length of the route ![]()
![]() The length of the route
The length of the route ![]()
![]() Length of the route
Length of the route ![]()
![]() The length of the route
The length of the route ![]()
![]() The length of the route
The length of the route ![]()
![]() The length of the route
The length of the route ![]()
An oriented tree with a root in vertex 1: