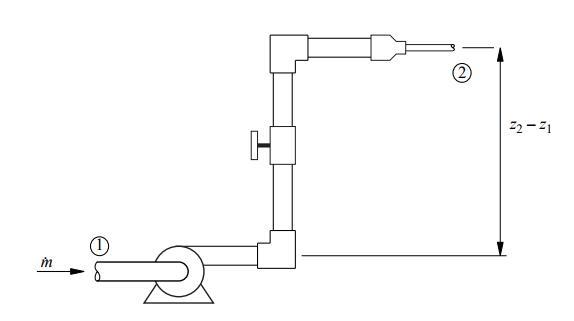
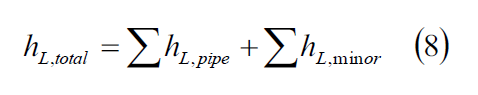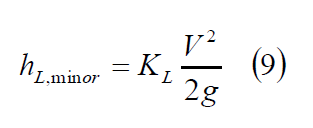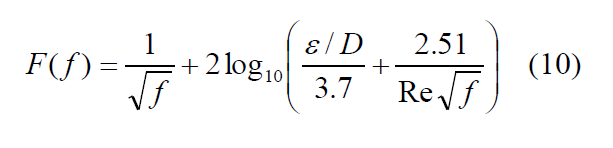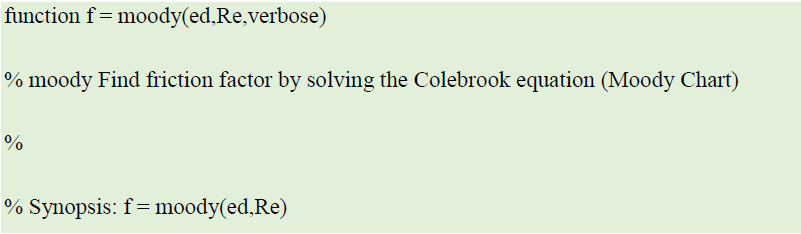Calculation of water head loss in the pipeline is very simple. In the head loss calculation example, we will consider in detail the calculation options. For hydraulic calculation of the pipeline, you can use the hydraulic calculator of the pipeline. From school physics lessons it is clear that the water flowing through the pipes, in any case, experiences resistance. The magnitude of this resistance depends on the flow velocity, the diameter of the pipe and the smoothness of its internal surface. The lower the resistance, the lower the flow speed and the greater the diameter and smoothness of the pipe. All these are taken into account while making head loss calculations.
The head loss calculation example presented here can help with assignment writing. The sample was made by an expert in engineering. Each writer’s experience in the field helps to deal with such tasks easily. However, you can find samples for other disciplines on our blog, for example, to get accounting homework help free online. Well, let’s start the calculation!
Head Loss Calculation
In this guide we will perform m head loss calculations, solve flow rate problems, generate system curves, and find the design point for a system and pump for pipe flow analysis.
Solution:
(Part 2)
Minor Losses
Minor losses are caused by elbows, valves, and other components that disrupt the fully-developed flow through the pipe. “Minor Loss” is a misnomer because in many practical systems, elbows, valves, and other components can account for a significant fraction of the head loss. Minor losses must be included in the head loss term in the energy equation. For most pipe runs there will be multiple minor loss elements connected by sections of straight pipe. The total loss can be represented by:
where hL pipe is the viscous loss in a straight section of pipe and hL,minor is a minor loss due to a fitting or other element. Note that the hL,pipe contributions are usually computed by assuming that the flow in the pipe section is fully developed. The empirical model for an individual minor loss is:
where KL is a loss coefficient.
Solve the Colebrook Equation using Matlab
Equation (7) cannot be solved analytically for f when ε/D and Re are given. However, if Equation (7) is rearranged as:
a numerical root-finding procedure can be used to find the f that makes F(f) = 0 when ε/D and Re are known.
The moody function finds the friction factor from the formulas used to create the Moody chart.

 The myMoody function uses the moody function to create a simplified version of the Moody chart.
The myMoody function uses the moody function to create a simplified version of the Moody chart.