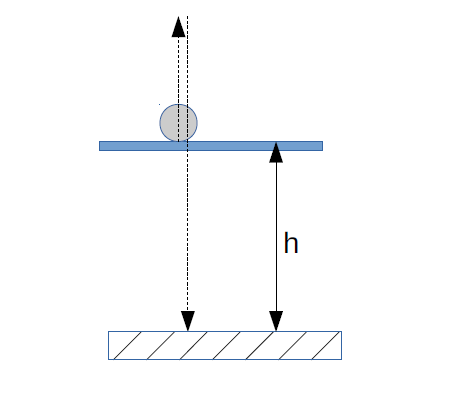
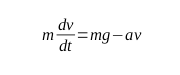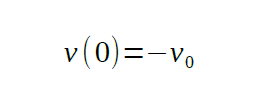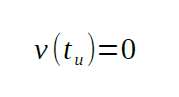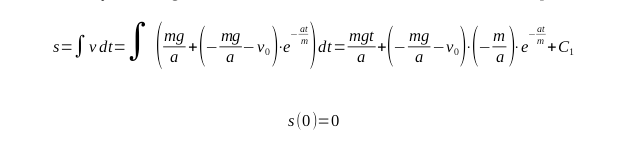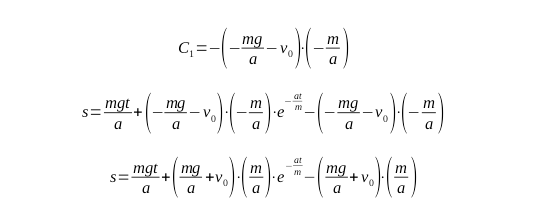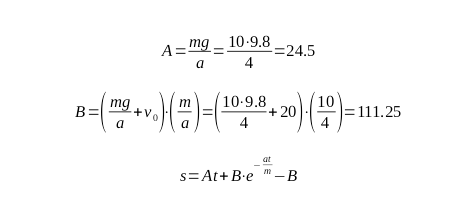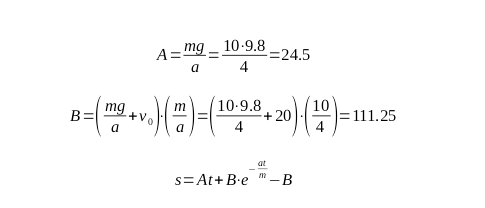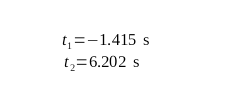An object that has a mass of m kg was thrown straight up from a platform which is h m above the ground. The initial velocity was
The air resistance is proportional to the velocity of the object and is equal to av N. Write down the equation for the distance traveled by the object at any time. Find the velocity of the object at the ground level for
Note: assume the object does not hit the platform when falling down.
Firstly, two cases should be considered:
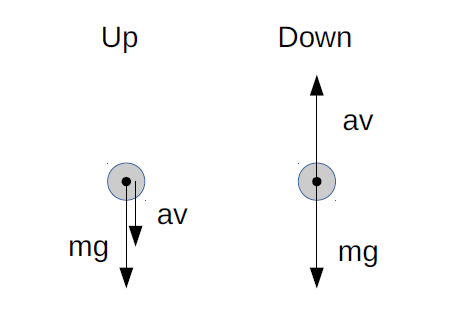
- The object moving up.
- The object falling down.
The free body diagram for it will be as follows:
Let’s take downward to be a positive direction.
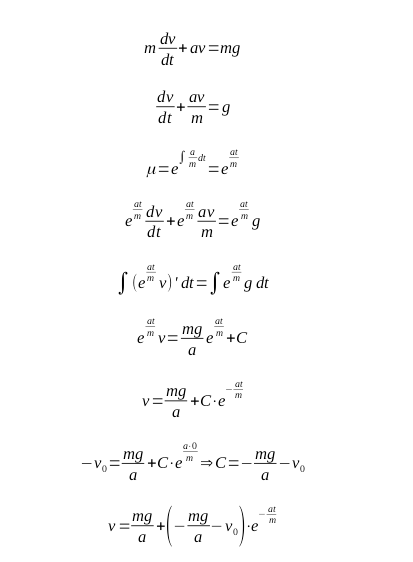
Knowing that the acceleration is the first derivative of the speed, let’s write down the basic equation for both cases (the resistance force is always opposite to the vector of velocity):
Initial Values:
Up:
Where
![]()
is the time at which the object will reach the highest point.
Solving the equation:
To find the velocity near the ground level, we need to determine the formula for the path traveled:
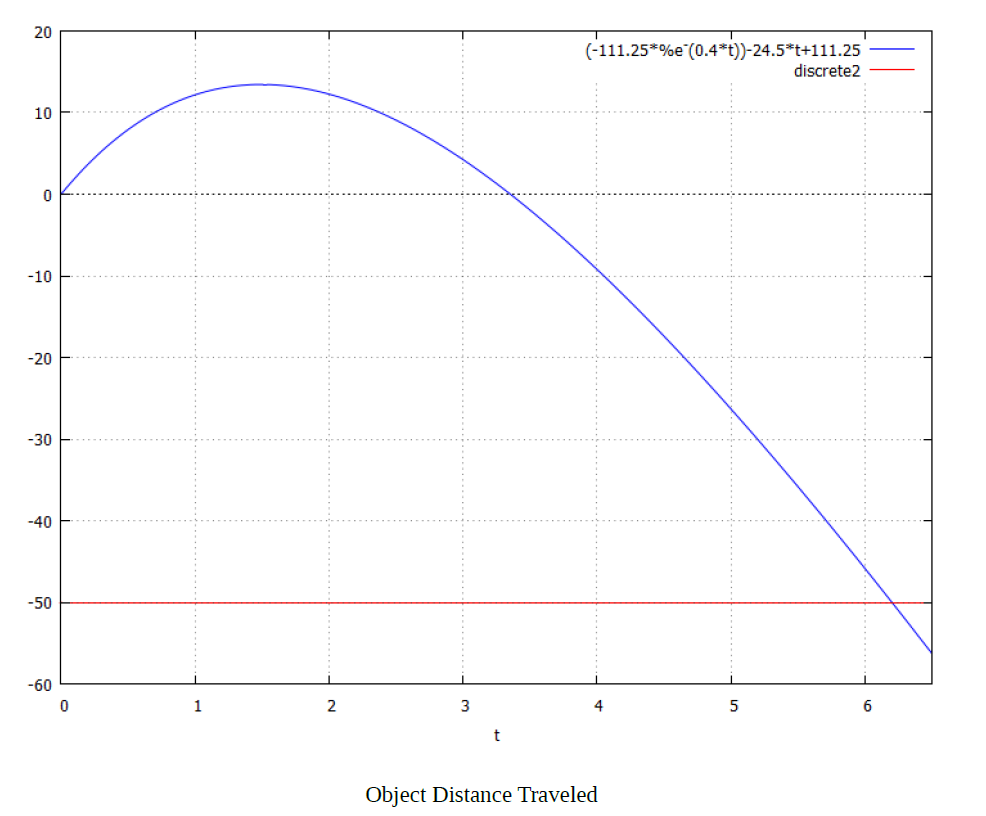
Now, we should find the time when the object falls on the ground. Let’s simplify the above equation:
Now, the following equation should be solved:
Knowing the exact values, the solution to the above equation can be found through iterative methods:
The value of t1 is not the correct value, as the time cannot be negative. So, t2 is the answer.
We hope that this task analysis of the speed of falling object problem was helpful and informative to you. This technical assignment was generated by our experts who specialize in kinematics and are ready to deliver an analysis of any technical field, including various branches of IT, engineering, physics, math, and chemistry. If you feel that this analysis of the velocity of a falling object is something that interests you, be sure to take a look at the other similar guides we make for students like you.
The AssignmentShark service has been delivering excellent academic assistance for over five years. We aid college and university students in their scientific life so that they have some more time for their personal and professional development. We provide the best assignment help at reasonable prices!